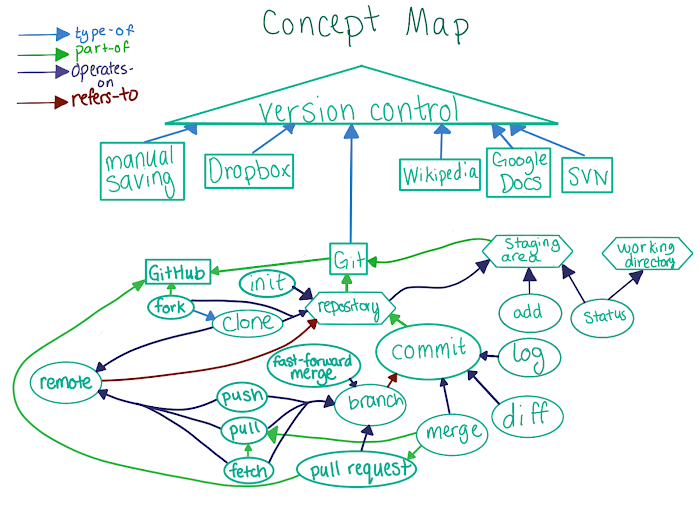
Http Status Code Overview
Reference: https://www.restapitutorial.com/httpstatuscodes.html
⭐︎ -> “Top 10” HTTP Status Code. More REST service-specific information is contained in the entry.
1XX Information
- 100 continue – Client should continue
- 101 switching protocols
- 102 processing (webDAV)
2XX Success
- ⭐︎200 OK – The request has succeeded.
General status code. Most common code used to indicate success.
- ⭐︎201 Created – A new resource has been created and should return a URI.
Successful creation occurred (via either POST or PUT). Set the Location header to contain a link to the newly-created resource (on POST). Response body content may or may not be present.