RB tree

2-3 tree & 2-4 tree

2-node: 1 key and 2 children 3-node: 2 keys and 3 children 4-node: 3 keys and 4 children

A (2,4) tree (also called 2-4 tree or 2-3-4 tree) is a multi-way search with the following properties:

• Node-Size Property: every internal node has at most four children
• Depth Property: all the external nodes have the same depth

insertion

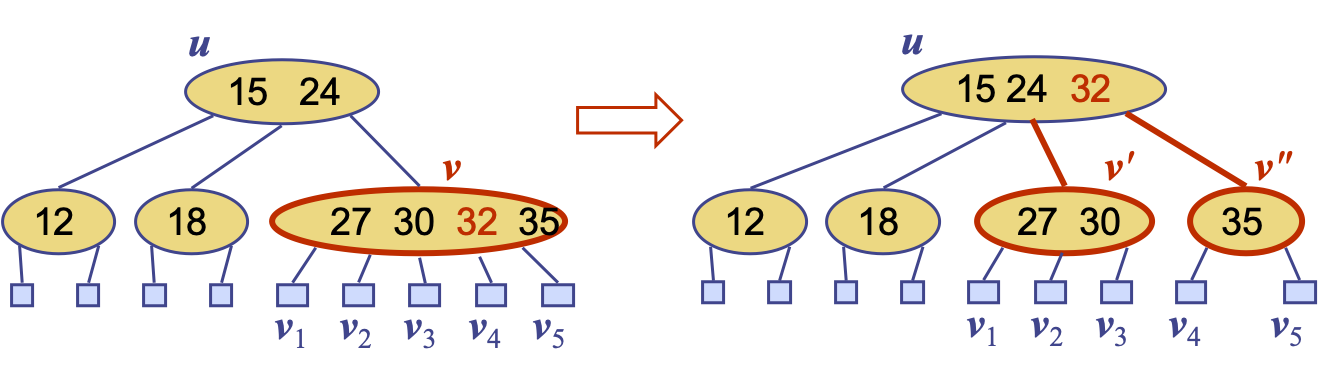
deletion

2-4 tree ==> RB tree

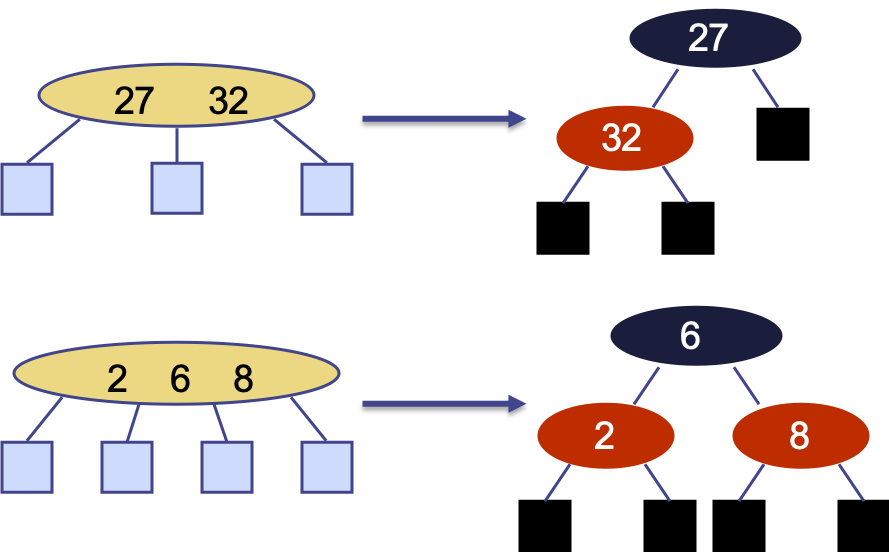
If break down 3-node and 4-node, 2-4 tree will become RB tree.

• 2-node ==> black node
• 3-node ==> left/right side red node and black node
• 4-node ==> two red node and a black node

RB tree represent a 2-4 tree in binary by providing a special balance strategy.

RB tree rotate

1
2
3
4

* New node --> X
* Parent --> P
* Grandparent --> G
* Parent sibling --> S

1. X must be red
2. while loop: P is red
   1. P is on the left of G
      1. S is red
         • Change P and S to black
         • Change G to red
         • Let G become X and back to while loop
      2. S is Black or Null
         • IF: X on the right of P. Then: Rotate_left()
         • Change P to black
         • Change G to red
         • Rotate_right()
   2. P is on the right of G
      1. S is red
         • Change P and S to black
         • Change G to red
         • Let G become X and back to while loop
      2. S is Black or Null
         • IF: X on the left of P. Then: Rotate_right()
         • Change P to black
         • Change G to red
         • Rotate_left()
3. ROOT = black // In case change root.

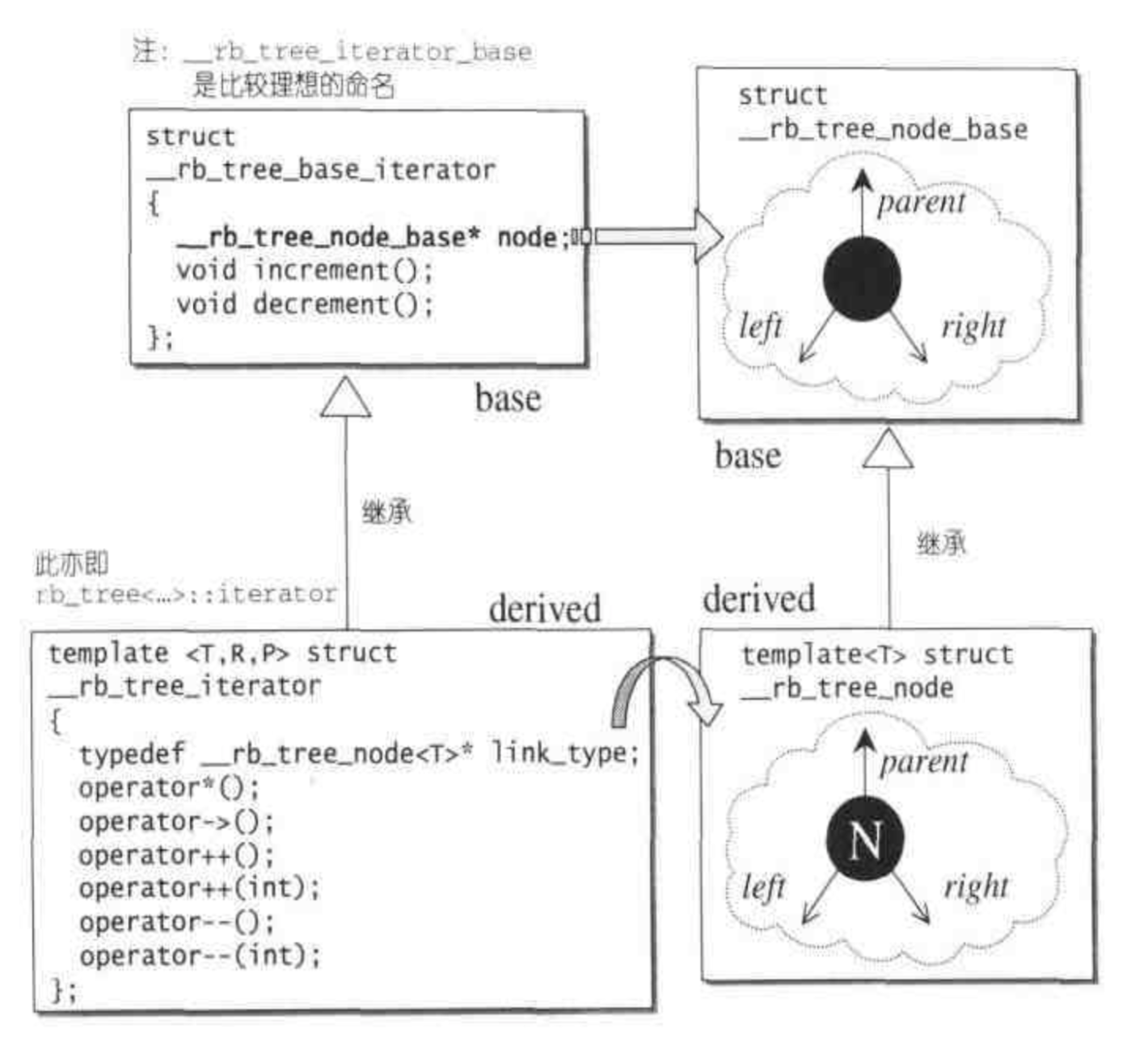
RB tree structure